- За затворена верига
- Единична верига и пълна верига
- Изчисляване на сечения ток за електрическа верига
- Варианти за пълна верига
- Влияние на закона върху дадена променлива
- Източник на ел. напрежение в пълна верига
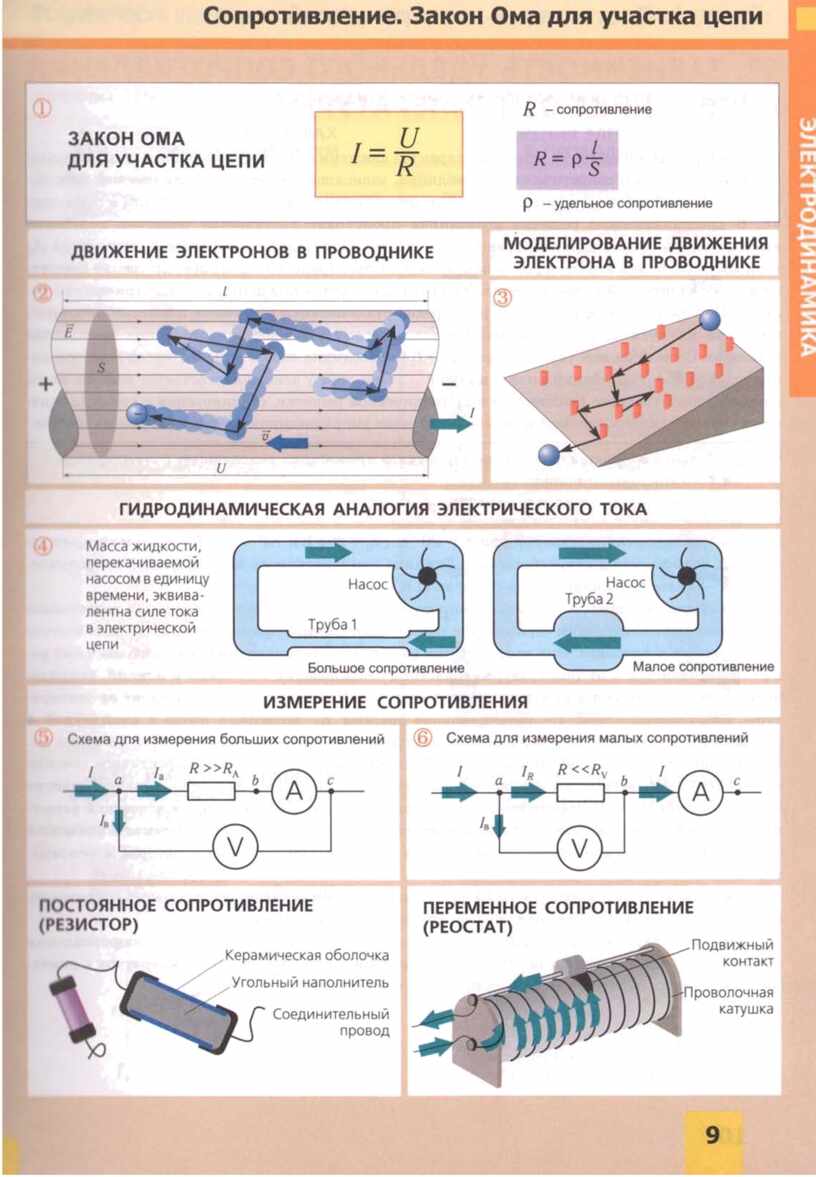
- R - електрическо съпротивление
- Секция с нехомогенна верига за постоянен ток
- Серийно и паралелно свързване на елементи
- Верига от последователно свързани съпротивителни елементи
- Верига от паралелно свързани съпротивителни елементи
- Интегрални и диференциални форми на закона
- Определяне на това какво представляват токът и съпротивлението
- Закон на Ом за променливия ток
- Когато законът на Ом срещне
- Закон на Кирхоф.
- Основни понятия
- Сила и напрежение
- Съпротивление на проводниците
- Тълкуване на закона на Ом
- Паралелно и последователно свързване
- Връзка в серия
- Паралелна връзка
- Какви са предимствата на паралелното и последователното свързване?
- Идеалният източник на ЕМП
- В диференциална форма
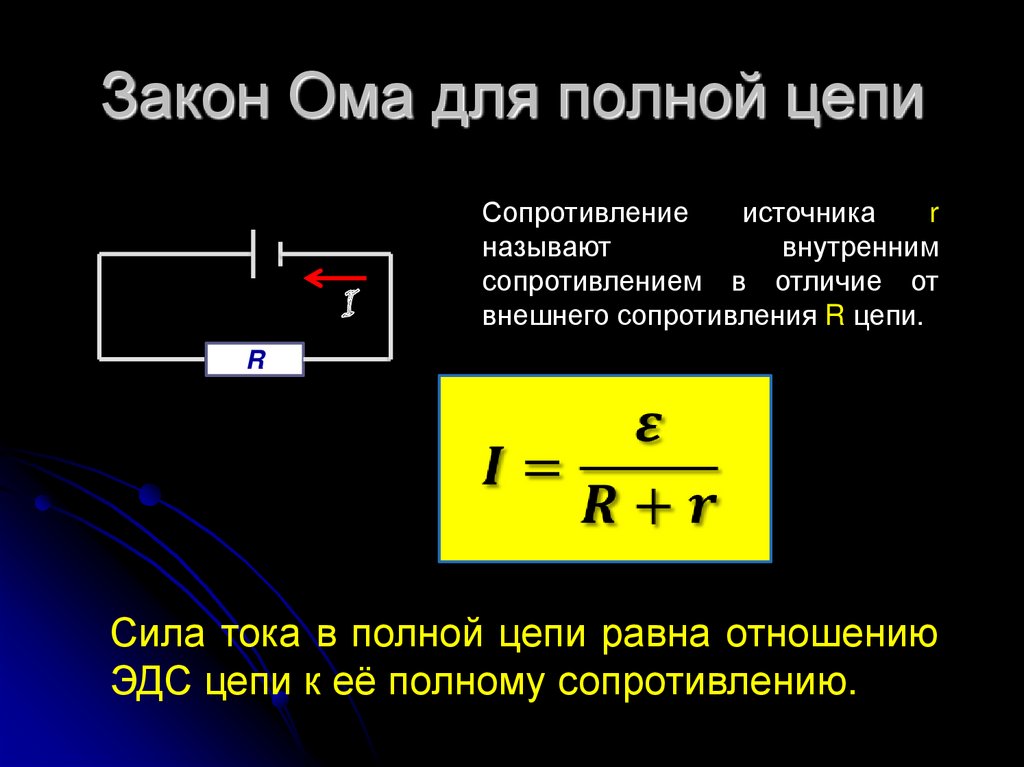
За затворена верига
Затворена верига означава затворена електрическа връзка, през която циркулира ток. Когато има поредица от проводници, които се свързват помежду си и затварят веригата, така че аз да преминавам от единия край на кръга до другия, това е затворена верига.
ЕМП (E) - обозначава се и се измерва във волтове и се отнася до напрежението, генерирано от батерия или магнитна сила съгласно закона на Фарадей, който гласи, че променливо във времето магнитно поле ще предизвика електрически ток.
След това: E = IR + Ir
E = I(R + r)
I = E/(R + r)
Където: r е съпротивлението на източника на ток.
Този израз е известен като закон на Ом за затворени вериги.
Нехомогенна верига
Единична верига и пълна електрическа верига
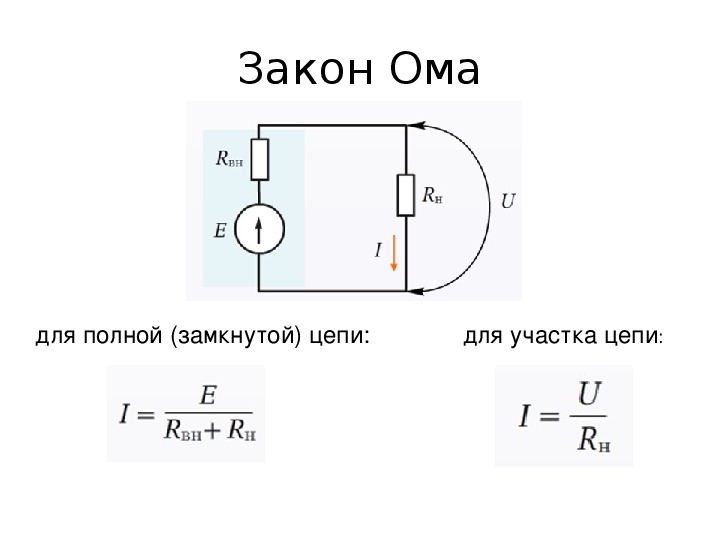
Законът на Ом, приложен към участък или цяла верига, може да се разглежда в две различни изчисления:
- Един кратък участък. е част от верига без източник на ЕМП.
- Пълна верига, състояща се от една или повече секции. Това включва и източник на ЕМП със собствено вътрешно съпротивление.
Изчисляване на тока в участък от верига
В този случай се прилага основната формула I = U/R, където I е токът, U е напрежението, а R е съпротивлението. От тази формула можем да формулираме общоприето тълкуване на закона на Ом:
Тази формулировка е в основата на много от другите формули, представени за така наречения "верижен" граф. Секторът P определя мощността, а секторите I, U и R извършват действията по отношение на тока, напрежението и съпротивлението.
Всеки израз, както основен, така и допълнителен, ви позволява да изчислите точните параметри на елементите, които ще се използват във веригата.
Специалистите, работещи с електрически вериги, извършват бързо определяне на някой от параметрите с помощта на показаната на фигурата техника на триъгълника.
При изчисленията трябва да се вземе предвид съпротивлението на проводниците, които свързват елементите на веригата един с друг. Тъй като те са изработени от различни материали, този параметър се различава във всеки случай. Ако трябва да се създаде пълна верига, основната формула се допълва с параметрите на източник на напрежение, например батерия.
Вариант на изчислението за пълна верига
Пълната верига се състои от отделни секции, които са комбинирани заедно с източник на напрежение (ел. енергия). По този начин съществуващото съпротивление на обекта се допълва от вътрешното съпротивление на свързания източник. Следователно основното тълкуване, разгледано по-рано, ще звучи по следния начин: I = U / (R + r). Тук вече е добавен съпротивителният индекс (r) на източника на ЕМП.
От гледна точка на чистата физика тази цифра се смята за много малка. На практика обаче специалистите трябва да го вземат под внимание при изчисляването на сложни вериги и схеми, тъй като допълнителното съпротивление оказва влияние върху точността на работа. Освен това структурата на всеки източник е много разнородна и в резултат на това съпротивлението може да бъде доста високо в някои случаи.
Горепосочените изчисления са направени по отношение на вериги за постоянен ток. При веригите за променлив ток действията и изчисленията са различни.
Действие на закона спрямо променлива стойност
При променливия ток съпротивлението на веригата ще бъде т.нар. импеданс, състоящ се от активно съпротивление и реактивен съпротивителен товар. Това се дължи на наличието на елементи с индуктивни свойства и на синусоидалната големина на тока. Напрежението също е променлива величина, която действа според законите за комутация.
Следователно променливотоковата верига по закона на Ом се проектира с оглед на специфични ефекти: водене или изоставане на тока и напрежението и наличие на ефективна и реактивна мощност. Реактивното съпротивление, от своя страна, включва индуктивни или капацитивни компоненти.
Всички тези явления ще съответстват на формулата Z = U / I или Z = R + J * (XL - XC), където Z е импеданс; R - активен товар; XL , XC - индуктивен и капацитивен товар; J - корекционен коефициент.
ЕМП на източника в пълна верига
За да възникне електрически ток в затворена верига, тази верига трябва да съдържа поне един специален елемент, в който да се извършва пренасянето на заряди между полюсите му. Силите, които пренасят заряди в този елемент, го правят срещу електрическото поле и следователно тяхното естество трябва да е различно от електрическото поле. Затова тези сили се наричат външни сили.
Фигура 1. Сили на трети страни във физиката.
Елементът от електрическата верига, в който се извършва работата на външните сили за прехвърляне на заряди срещу електрическото поле, се нарича източник на ток. Основната му характеристика е големината на външната сила. Тя се характеризира със специална мярка - електродвижеща сила (ЕДС) - и се означава с $\mathscr{E}$.
Стойността на ЕМП на източник на ток е равна на отношението на външната сила върху преноса на заряд към стойността на заряда:
$$\mathscr{E}={A_{ст}\over q}$$
Тъй като значението на ЕМП е много сходно с това на електрическото напрежение (спомнете си, че напрежението е отношението на работата, извършена от електрическо поле, пренасящо заряд, към стойността на този заряд), ЕМП се измерва във волтове, както и напрежението:
$$1V={JouleKl}$$
Втората най-важна електрическа характеристика на реалния източник на ток е неговото вътрешно съпротивление. Когато зарядите се пренасят между клемите, те взаимодействат с веществото на източника на ЕМП и следователно източникът на електрически ток също оказва известно съпротивление. Вътрешното съпротивление, както и нормалното съпротивление, се измерва в омове, но се обозначава с малката латинска буква $r$.

Фигура 2. Примери за източници на ток.
R - електрическо съпротивление
Съпротивлението е обратна величина на напрежението и може да се сравни с ефекта от движението на тяло срещу движението в течаща вода. Единицата за R е "Ом", която се обозначава с главната гръцка буква "Омега".
Обратното на съпротивлението (1 /R) се нарича проводимост, която измерва способността на даден обект да провежда заряд, изразена в единици на Сименс.
Използваната геометрично независима стойност се нарича съпротивление и обикновено се обозначава с гръцкия символ r.
Допълнителна информация. Законът на Ом помага да се установят три важни показателя за работата на електрическата мрежа, което опростява изчисленията на мощността. Тя не се прилага за еднопосочни мрежи с елементи като диоди, транзистори и т.н. И също така не се прилага за нелинейни елементи, примери за които са тиристорите, тъй като стойността на съпротивлението на тези елементи се променя при различни данни за напрежението и тока.
При по-високи честоти разпределеното поведение става доминиращо. Същото се случва и с много дългите електропроводи. Дори и при толкова ниска честота като 60 Hz много дълга преносна линия, например 30 km, има разпределен характер. Основната причина за това е, че активните електрически сигнали, които се разпространяват във веригите, са електромагнитни вълни, а не волтажи и ампери, които са заразени от електромагнитната вълна. Проводниците просто служат като водачи на вълните. Така например един коаксиален кабел ще покаже Z = 75 ома, дори ако съпротивлението му при постоянен ток е незначително.
Законът на Ом е основен закон на електротехниката. Той има голям брой практически приложения във всички електрически вериги и електронни компоненти.
Най-често срещаните приложения на закона на Ом са:
- Мощността, подавана към електрически нагревател. Като се има предвид съпротивлението на намотката на нагревателя и приложеното напрежение, може да се изчисли мощността, която трябва да се приложи към този нагревател.
- Избор на предпазител. Те са защитни компоненти, които се свързват последователно с електронни устройства. Предпазителите/CB се изчисляват в ампери. Номиналният ток на предпазителя се изчислява по закона на Ом.
- Проектиране на електронни устройства. Електронните устройства, като например лаптопи и мобилни телефони, се нуждаят от захранване с постоянен ток с определен номинален ток. Типичните батерии за мобилни телефони се нуждаят от 0,7-1 А. Резисторът се използва за управление на скоростта на тока, протичащ през тези компоненти. Законът на Ом се използва за изчисляване на номиналния ток в типична верига.
Навремето изводите на Ом са били катализатор за нови изследвания в областта на електричеството и не са загубили значението си и до днес, когато са в основата на съвременната електротехника. През 1841 г. Ом е удостоен с най-високата награда на Кралското дружество - медал "Копли", а терминът "Ом" е признат като единица за съпротивление още през 1872 г.
Секция с нехомогенна верига за постоянен ток
Нехомогенната част на веригата има източник на ток в допълнение към проводниците и елементите. Нейната ЕМП трябва да се вземе предвид при изчисляването на общия ток в този раздел.
Съществува формула, която определя основните параметри и процеси в нехомогенен участък: q = q0 x n x V. Параметрите му се характеризират, както следва:
- В процеса на движение на зарядите (q) те придобиват определена плътност. Стойностите зависят от силата на тока и площта на напречното сечение на проводника (S).
- При определена концентрация (n) е възможно да се определи точно броят на единичните заряди (q0), които са били изместени за единица време.
- За целите на изчисленията обикновено се приема, че проводникът е цилиндрично сечение с определен обем (V).
Когато един проводник е свързан с батерия, след известно време тя се разрежда. С други думи, движението на електроните постепенно се забавя и накрая напълно спира. За това спомагат молекулярната решетка на проводника, която действа срещу него, сблъсъкът на електроните помежду им и други фактори. За да се преодолее това съпротивление, трябва да се приложат определени допълнителни външни сили.
При изчисленията тези сили се добавят към силата на Кулон. Освен това, за да се прехвърли единичен заряд q от първата към втората точка, трябва да се извърши работата A1-2 или просто A12. За тази цел се създава потенциална разлика (ϕ1 - ϕ2). Под действието на източник на постоянен ток се създава ЕМП, която премества зарядите по веригата. Големината на общото напрежение ще се състои от всички сили, отбелязани по-горе.
Полярността на връзката с източника на постоянен ток трябва да се вземе предвид при изчисленията. С промяната на клемите се променя и ЕМП, която ускорява или забавя движението на зарядите.
Свързване на елементи последователно и паралелно
Елементите на една електрическа верига (участък от веригата) обикновено са свързани последователно или паралелно.
Съответно всеки тип връзка се съпровожда от различен тип протичане на ток и подаване на напрежение. Законът на Ом също се прилага по различен начин в зависимост от това как са свързани елементите.
Верига от последователно свързани резистивни елементи
В случай на последователно свързване (участък от верига с два компонента) се използва формулировката:
- I = I1 = I2 ;
- U = U1 + U2 ;
- R = R1 + R2
Тази формулировка ясно показва, че независимо от броя на последователно свързаните съпротивителни елементи, токът, протичащ в даден участък от веригата, не променя стойността си.
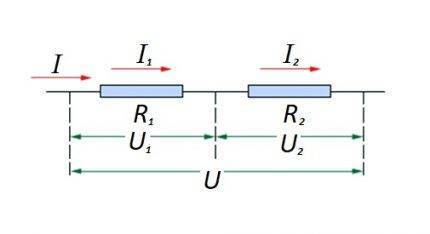 Свързване на резистивните елементи последователно в участък от веригата, един след друг. За този вариант се прилага различен закон за изчисление. В диаграмата: I, I1, I2 - поток на тока; R1, R2 - съпротивителни елементи; U, U1, U2 - приложено напрежение
Свързване на резистивните елементи последователно в участък от веригата, един след друг. За този вариант се прилага различен закон за изчисление. В диаграмата: I, I1, I2 - поток на тока; R1, R2 - съпротивителни елементи; U, U1, U2 - приложено напрежение
Големината на напрежението, приложено към активните съпротивителни компоненти на веригата, е сумата и съставлява общата стойност на източника на ЕМП.
Напрежението върху всеки отделен компонент е: Ux = I * Rx.
Общото съпротивление трябва да се разглежда като сума от стойностите на всички съпротивителни компоненти във веригата.
Верига от паралелно свързани съпротивителни елементи
В случай на верига от паралелно свързани съпротивителни компоненти се счита, че по отношение на закона на Ом на немския физик е вярно следното
- I = I1 + I2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Не е изключено да се направят участъци от веригата от "смесен" тип, когато се използва паралелно и последователно свързване.
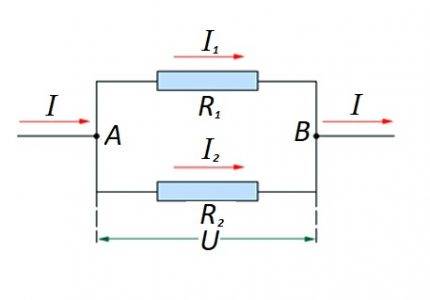 Свързване на съпротивителните елементи в участък от веригата успоредно един на друг. За този вариант се прилага специфичен закон за изчисление. В диаграмата: I, I1, I2 - поток на тока; R1, R2 - резистивни елементи; U - приложено напрежение; A, B - входни/изходни точки
Свързване на съпротивителните елементи в участък от веригата успоредно един на друг. За този вариант се прилага специфичен закон за изчисление. В диаграмата: I, I1, I2 - поток на тока; R1, R2 - резистивни елементи; U - приложено напрежение; A, B - входни/изходни точки
За тези варианти изчислението обикновено се извършва чрез първоначално изчисляване на номиналното съпротивление на паралелната връзка. След това към резултата се прибавя номиналната стойност на последователния резистор.
Интегрални и диференциални форми на закона
Всички горепосочени точки за изчисление се отнасят за условия, при които в електрическите вериги се използват проводници с, така да се каже, "хомогенна" структура.
В практиката обаче нерядко се срещат вериги, в които структурата на проводниците се променя в различните области. Използват се например проводници с по-голямо напречно сечение или, обратно, по-малки проводници, изработени от различни материали.
За да се отчетат тези разлики, има вариант на така наречения "диференциално-интегрален закон на Ом". За един безкрайно малък проводник нивото на плътността на тока се изчислява като функция на напрежението и стойността на специфичната проводимост.
Диференциалното изчисление се извършва по формулата: J = ό * E
За изчисляване на интеграла се използва съответно формулата: I * R = φ1 - φ2 + έ
Тези примери обаче са по-скоро по-близо до школата на висшата математика и в реалната практика на обикновения електротехник те не се прилагат.
Нека разгледаме тока и съпротивлението
Нека да започнем с понятието за електрически ток. Накратко, електрическият ток в металите е насочено движение на електрони, които са отрицателно заредени частици. Обикновено те са представени като малки кръгове. В състояние на покой те се движат хаотично, като постоянно променят посоката си. При определени условия - потенциална разлика - тези частици започват да се движат в определена посока. Това движение е електрически ток.
За да стане по-ясно, можем да сравним електроните с вода, разлята върху самолет. Докато самолетът е неподвижен, водата не се движи. Но щом се появи наклон (потенциална разлика), водата се раздвижва. Приблизително същото е и с електроните.
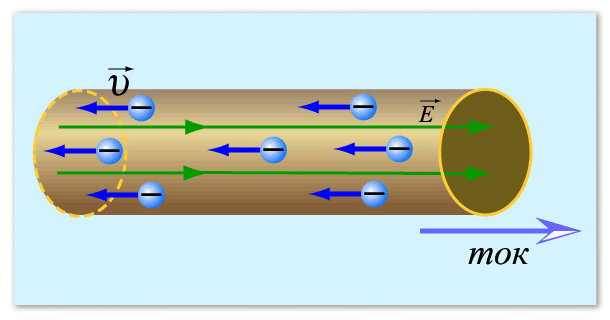
Приблизително така можете да си представите електрическия ток
Сега трябва да разберем какво е съпротивлението и защо то е в обратна зависимост от тока: колкото по-голямо е съпротивлението, толкова по-малък е токът. Както знаете, електроните се движат по проводник. Обикновено това са метални проводници, тъй като металите имат добра способност да провеждат електрически ток. Знаем, че металът има плътна кристална решетка: много частици, които са разположени на близко разстояние и са свързани помежду си. Електроните, които си проправят път между атомите на метала, се блъскат в тях, което затруднява движението им. Това помага да се илюстрира съпротивлението, което оказва един проводник. Сега става ясно защо колкото по-голямо е съпротивлението, толкова по-малък е токът - колкото повече са частиците, толкова по-трудно се придвижват електроните и толкова по-бавно го правят. Това изглежда е решено.
Ако искате да проверите тази зависимост експериментално, намерете променлив резистор, свържете последователно резистор - амперметър - източник на ток (батерия). Препоръчително е също така да поставите превключвател във веригата - обикновен превключвател.
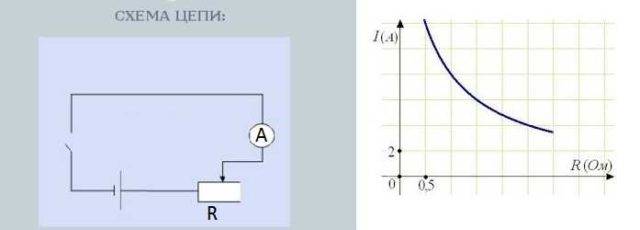
Схема за изпитване на съпротивлението на тока
Завъртете копчето на резистора, за да промените съпротивлението. Показанията на амперметъра, който измерва силата на тока, също ще се променят. Колкото по-голямо е съпротивлението, толкова по-малко се отклонява стрелката - толкова по-малък е токът. Колкото по-ниско е съпротивлението, толкова повече се отклонява стрелката - повече ток.
Зависимостта на тока от съпротивлението е почти линейна, т.е. графиката показва почти права линия. Защо тя е почти линейна, е отделна тема, но това е друга история.
Закон на Ом за променлив ток
При изчисляване на вериги за променлив ток вместо съпротивление се въвежда понятието "съпротивление". Импедансът се обозначава с буквата Z и включва съпротивлението на товара Ra и реактивното съпротивление X (или Rr). Това се дължи на формата на синусоидалния ток (и на токове с всякаква друга форма) и на параметрите на индуктивните елементи, както и на законите за превключване:
- Токът във верига с индуктивност не може да се променя мигновено.
- Напрежението във верига с капацитет не може да се променя мигновено.
Поради това токът започва да изостава или да предхожда напрежението, а общата мощност се разделя на активна и реактивна мощност.
U=I/Z
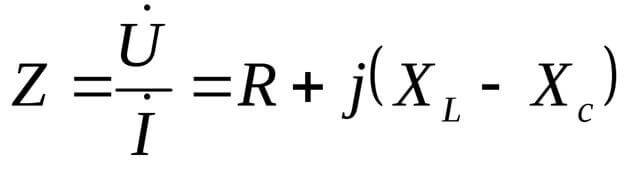
XL и XC - са компонентите на реактивния товар.
Поради това се въвежда стойността coSF:
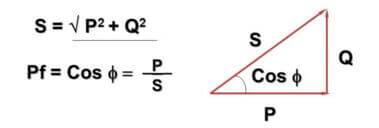
Тук - Q е реактивната мощност, дължаща се на променливия ток и индуктивно-капацитивните компоненти, P е активната мощност (разпределена на активните компоненти), S е общата мощност, cosF е коефициентът на мощността.
Може би сте забелязали, че формулата и нейното представяне се припокриват с Питагоровата теорема. Това наистина е вярно и ъгълът F зависи от това колко голяма е реактивната компонента на товара - колкото по-голяма е тя, толкова по-голям е той. На практика това води до факта, че реално протичащият ток в мрежата е по-голям от този, отчитан от домакинския електромер, но предприятията плащат за цялата мощност.
В този случай съпротивлението се представя в сложна форма:
Тук j е имагинерната единица, която е характерна за комплексната форма на уравненията. По-рядко се нарича i, но в електротехниката се нарича и ефективна стойност на променливия ток, така че за да се избегне объркване, е по-добре да се използва j.
Въображаемата единица е равна на √-1. Логически погледнато, не съществува число, което, когато е повдигнато на квадрат, може да даде отрицателен резултат "-1".
Когато се сблъскате със закона на Ом
Създаването на идеални условия не е лесно. Дори при чистите проводници електрическото съпротивление се променя в зависимост от температурата. Намаляването му намалява активността на молекулите на кристалната решетка, което улеснява движението на свободните заряди. При определено ниво на "замразяване" се появява ефектът на свръхпроводимост. Обратният ефект (влошаване на проводимостта) се наблюдава при нагряване.
В същото време електролитите, металите и някои видове керамика запазват електрическото си съпротивление независимо от плътността на тока. Стабилността на параметрите при поддържане на определен температурен режим позволява прилагането на формулите на закона на Ом без допълнителни корекции.
Полупроводниковите материали и газовете имат променливо електрическо съпротивление. Този параметър се влияе значително от интензитета на тока в изпитвания обем. За изчисляване на работните характеристики трябва да се използват специализирани изчислителни методи.
Ако се разглежда променлив ток, методиката за изчисление се коригира. В този случай трябва да се вземе предвид наличието на реактивни компоненти. Ако съпротивлението е съпротивително по природа, могат да се приложат разгледаните по-горе техники за изчисление, основани на формулите на закона на Ом.
Закони на Кирхоф.
Разпределение на
на токовете в електрическа верига
се управлява от първия закон на Кирхоф,
и разпределението на напреженията върху
се управлява от втория закон на Кирхоф.
Закони на Кирхоф
заедно със закона на Ом са основните закони
в теорията на електрическите вериги.
Първият
Закон на Кирхоф:
Алгебричен
сумата от токовете в даден възел е равна на нула:
i
= 0 (19)
Къде:
i
- е броят на клоновете, които се събират в този възел.
Това означава, че сумата
важи за токовете в клоновете
които се събират във въпросния възел
възел.
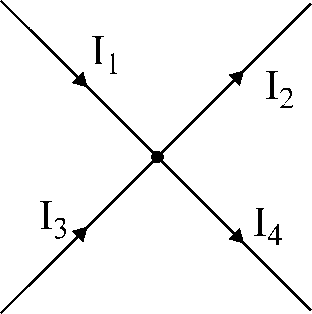
Фигура 17. Илюстрация на .
по първия закон на Кирхоф.
Номер
уравненията, които трябва да се направят от първия
Първият закон на Кирхоф се определя от формулата:
Noup
= Ny
– 1,
Къде:
Nu
- е броят на възлите във въпросната схема.
Знаците на токовете в
в уравнението се основават на избрания
положителна посока. Признаците на
са идентични, ако токовете имат еднакви
са ориентирани по отношение на дадената
възел.
Например,
За възела, показан на фигура 17:
да зададем знаци
знаци "+", а за токовете, изтичащи от възела - знаци
«-».
Тогава уравнението
съгласно първия закон на Кирхоф ще се запише
както следва:
I1
- I2
+ I3
- I4
= 0.
Уравнения,
Конструиран съгласно първия закон на Кирхоф,
се наричат възлови уравнения.
Този
законът изразява факта, че в даден възел
електрическият заряд не се натрупва
нито се разсейва. Сумата от електрическите
на електрическите заряди, пристигащи в даден възел, е равна на сумата от
на зарядите, които напускат възела в същата
за същия период от време.
Втори
Втори закон на Кирхоф:
Алгебричен
сумата на електродвижещите сили в затворена верига
е равна на алгебричната сума на напрежението
на падовете на напрежение върху елементите на тази верига:
Ui
=
Ei
IiRi=Ei(20)
Къде:
i
- е номерът на елемента (съпротивление или
източник на напрежение) във въпросната верига
на въпросната верига.
**Число
на уравнения в съответствие с второто
Вторият закон на Кирхоф е даден с формулата:
Nup
= Nb
- Ну
+ 1 - Ne.d.s.
Къде:
Nb
- е броят на разклоненията във веригата;
Nu
- е броят на възлите;
Ne.d.s.
- брой на идеалните източници на електромагнитни въздействия.
Фигура 18. Илюстрация на
на втория закон на Кирхоф.
За да
да запишете правилно втория закон на Кирхоф
Втори закон на Кирхоф за дадена верига
трябва да се спазват следните правила:
-
произволно
Изберете посоката, в която ще се обхожда цикълът,
напр. по посока на часовниковата стрелка (фиг.18). -
Падът на напрежение е същият като този на веригата.
и падовете на напрежение, които са в една и съща
посока с избраната посока
трябва да се запишат в израза с
със знак "+"; ако напреженията a.d.s. и d.t.
не съвпадат с посоката на обходния път
посока, то те трябва да бъдат предшествани от знака "+".
«-».
Например,
За веригата от фигура 18 важи вторият закон на Кирхоф
ще бъде записана по следния начин:
U1
- U2
+ U3
= E1
- E3
- E4
(21)
Уравнение (20) може да бъде
може да се препише във вида:
(Ui
- Ei)
= 0 (22)
Къде:
(U
- E)
- е напрежението на клона.
Следователно,
Вторият закон на Кирхоф може да се формулира така
както следва:
Алгебричен
сумата от напреженията на клоновете във всеки
на всяка затворена верига е нула.
Потенциалът
диаграмата, разгледана по-рано, служи като
графична интерпретация на втората формула на Кирхоф
Втори закон на Кирхоф.
Проблем 1.
В
В схемата на фиг.1 токовете I1
и аз3,
Съпротивление и емоции. Определете токовете
I4,
I5,
I6
; напреженията между точките a
и b
ако I1
= 10mA
I3
= -20 mA
R4
= 5kOhm,
E5
= 20B,
R5
= 3kOhm,
E6
= 40B,
R6
= 2kOhm.
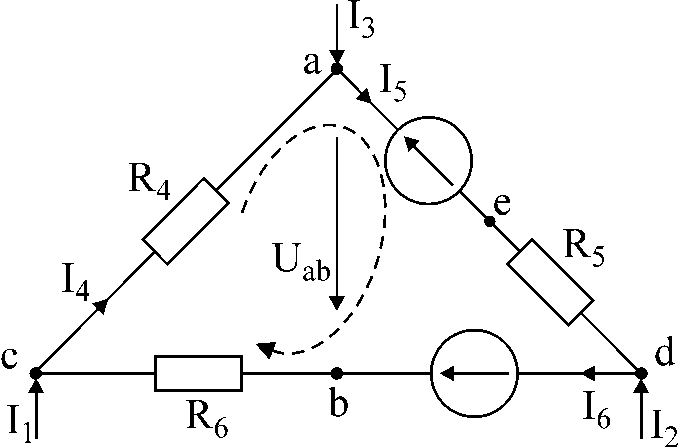
Фиг.1
Решение:
-
За даден
на дадена верига се съставят две уравнения в съответствие с
според първия закон на Кирхоф и един според
вторият. Посоката на заобикаляне на веригата
е отбелязан със стрелка.

В
в резултат на решението получаваме: I6
= 0; I4
= 10mA;
I5
= -10mA
-
Задайте
посоката на напрежението между точките
a
и b
от точка "a"
до точка "b"
- Uab.
Намираме това напрежение от уравнението по следния начин
на втория закон на Кирхоф:
I4R4
+ Uab
+ I6R6
= 0
Uab
= - 50B.
Задача № 2.
За
Фигура 2 съставя уравненията според Кирхоф
Законите на Кирхоф и определяне на неизвестните
точки.
Дадено:
I1
= 20mA;
I2
= 10mA
R1
= 5kOhm,
R3
= 4kOhm,
R4
= 6kOhm,
R5
= 2kOhm,
R6
= 4kOhm.
Фигура 2
Решение:
Броят на възлите
е 3, а броят на уравненията на контура
– 1.
Запомнете!
В уравнението на втория
Закон на Кирхоф, изберете верига
който не включва никакви източници на ток.
Посоката на веригата е показана на фигурата.
В
За дадена верига токовете на клоновете I1
и аз2.
Неизвестно
токове
I3,
I4,
I5,
I6.

Решаване на проблеми
на системата, получаваме: I3
= 13,75 mA;
I4
= -3,75 mA;
I5
= 6,25 mA;
I6
= 16,25 mA.
Основни понятия
Електрическият ток протича, когато затворена верига позволява на електроните да се движат от висок потенциал към по-нисък във веригата. С други думи, токът се нуждае от източник на електрони, който има енергията да ги задвижва, както и от точка на връщане на отрицателните им заряди, която се характеризира с тяхната оскъдност. Като физическо явление токът в една верига се характеризира с три основни величини:
- напрежение;
- ампераж;
- Съпротивление на проводника, през който се движат електроните.
Сила и напрежение
Токът на тока (I, измерван в ампери) е количеството електрони (заряд), които преминават през дадено място във веригата за единица време. С други думи, измерването на I е определяне на броя на електроните в движение.
Важно е да се разбере, че терминът се отнася само за движение: статичните заряди, например на клемите на несвързана батерия, нямат измерима стойност на I. Токът, който тече в една посока, се нарича постоянен ток (DC), а този, който периодично променя посоката си, се нарича променлив ток (AC). Напрежението може да се илюстрира с явление като налягането или разликата в потенциалната енергия на обектите, дължаща се на гравитацията.
За да се създаде този дисбаланс, трябва предварително да се изразходва енергия, която ще се реализира в движение при подходящи обстоятелства. Например при падане на товар от височина работата се извършва чрез повдигането му; при галваничните батерии потенциалната разлика на клемите се създава чрез преобразуване на химическа енергия; при генераторите - чрез въздействието на електромагнитното поле
Напрежението може да се илюстрира с явление като налягането или разликата в потенциалната енергия на даден обект, дължаща се на действието на гравитацията. За да се създаде този дисбаланс, трябва предварително да се изразходва енергия, която ще се реализира в движение при подходящи обстоятелства. Например при падането на товар от височина се извършва работата по повдигането му, при галваничните батерии потенциалната разлика на клемите се създава чрез преобразуване на химическата енергия, а при генераторите - чрез въздействието на електромагнитното поле.
Съпротивление на проводниците
Колкото и добър проводник да е, той никога няма да позволи на електроните да преминат през него без някакво съпротивление на движението им. Съпротивлението може да се разглежда като аналог на механичното триене, въпреки че това сравнение не е перфектно. Когато през проводник протича ток, част от потенциалната разлика се превръща в топлина, така че върху резистора винаги ще има пад на напрежение. Електрическите отоплителни уреди, сешоарите и други подобни устройства са предназначени единствено за разсейване на електрическа енергия под формата на топлина.
По-просто казано, съпротивлението (означено като R) е мярка за това доколко е възпрепятстван потокът на електрони в дадена верига. Тя се измерва в омове. Проводимостта на резистор или друг елемент се определя от две свойства
- геометрия;
- материала.
Формата е от изключително значение, както е видно от хидравличната аналогия: много по-трудно е да се прокара вода през дълга и тясна тръба, отколкото през къса и широка. Материалите играят решаваща роля. Например електроните могат да се движат свободно в медна жица, но не могат да преминат през изолатори като гума, независимо от формата им. Освен геометрията и материала има и други фактори, които влияят върху проводимостта.
Тълкуване на закона на Ом
За да могат зарядите да се движат, веригата трябва да бъде затворена. При липса на допълнителна сила токът не може да съществува дълго. Потенциалите бързо ще се изравнят. Необходим е допълнителен източник (генератор, батерия), за да се поддържа веригата в действие.
Пълната верига съдържа общото електрическо съпротивление на всички компоненти. За точни изчисления се вземат предвид загубите в проводниците, съпротивителните елементи и захранването.
Колко напрежение да се приложи за даден интензитет на тока се изчислява по формулата:
U = I * R.
Другите параметри на веригата се определят по същия начин, като се използват съотношенията, разгледани по-горе.
Паралелни и последователни връзки
В електричеството елементите се свързват последователно, един след друг, или паралелно, когато няколко входа са свързани към една точка, а изходите от същите елементи са свързани към друга точка.
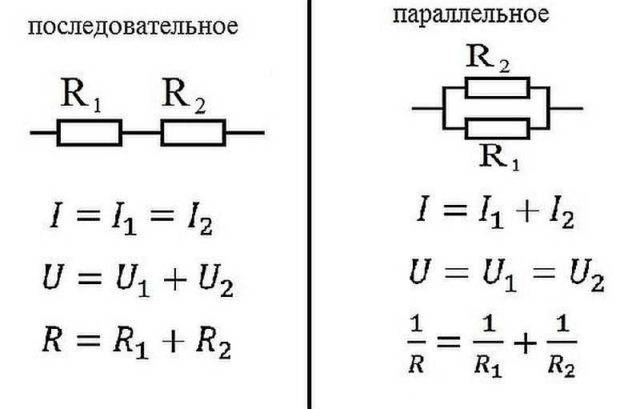
Закон на Ом за паралелно и последователно свързване
Връзка в серия
Как действа законът на Ом в тези случаи? При последователно свързване токът, протичащ през верига от елементи, е един и същ. Напрежението на участък от верига с последователно свързани елементи се отчита като сума от напреженията на всеки участък. Как може да се обясни това? Токът, протичащ през клетката, представлява прехвърляне на част от заряда от една част на клетката към друга. С други думи, това е определен обем работа. Размерът на тази работа е напрежение. Това е физическото значение на напрежението. Ако това е ясно, нека продължим.
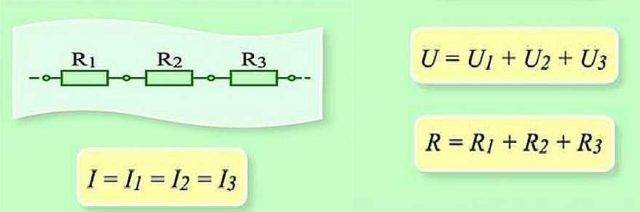
Серийно свързване и параметрите на този участък от веригата
Когато свързвате последователно, трябва да прехвърлите заряда през всеки елемент последователно. И за всеки елемент това е определено "количество" работа. И за да се определи количеството работа в цялата верига, трябва да се събере работата на всеки елемент. Така че общото напрежение е сумата от напреженията на всеки елемент.
По същия начин - чрез сумиране - се намира общото съпротивление на даден участък от веригата. Как може да си представим това? Токът протича през верига от елементи, като преодолява всички последователни съпротивления. Един след друг. Така че, за да определите съпротивлението, което е преодолял, трябва да съберете съпротивленията. Точно толкова. Математическото заключение е по-сложно, но така е по-лесно да се разбере механизмът на този закон.
Паралелна връзка
Паралелна връзка е, когато началата на проводниците/елементите се събират в една точка, а краищата им са свързани в друга. Нека се опитаме да обясним законите, които са валидни за този тип връзка. Нека започнем с текущите. В точката на свързване на елементите се подава ток с определена големина. То се разделя, като преминава през всички проводници. От това следва, че общият ток в даден обект е равен на сумата от тока във всеки от елементите: I = I1 + I2 + I3.
Сега относно напрежението. Ако напрежението е работата по преместването на заряд, то работата, необходима за преместването на един заряд, ще бъде еднаква за всяка клетка. Това означава, че напрежението на всеки паралелно свързан елемент ще бъде едно и също. U = U1=U2=U3. Не е толкова забавно и нагледно, колкото обяснението на закона на Ом за участък от веригата, но е разбираемо.
Закони за паралелна връзка
При съпротивата нещата са малко по-сложни. Нека въведем понятието проводимост. Това е характеристика, която показва колко лесно или трудно е заряда да премине през този проводник. Ясно е, че колкото по-ниско е съпротивлението, толкова по-лесно преминава токът. Следователно проводимостта - G - се изчислява като обратна стойност на съпротивлението. Във формулата тя изглежда така: G = 1/R.
Защо говорихме за проводимостта? Тъй като общата проводимост на участък с паралелно разположени елементи е равна на сумата от проводимостите за всеки от участъците. G = G1 + G2 + G3 - лесно за разбиране. Колко лесно токът ще премине през този възел от паралелни елементи зависи от проводимостта на всеки от елементите. Оказва се, че трябва да ги съберете.
Сега можем да преминем към съпротивлението. Тъй като проводимостта е обратна на съпротивлението, можем да получим следната формула: 1/R = 1/R1 + 1/R2 + 1/R3.
Какво ни дава паралелното и последователното свързване?
Теоретичните знания са добри, но как да ги приложим на практика? Всички видове елементи могат да се свързват паралелно и последователно. Но ние разгледахме само най-простите формули, които описват линейни елементи. Линейните елементи са резистори, наричани още "съпротивления". Ето как можете да използвате наученото:
Ако не разполагате с голям резистор, но имате няколко "по-малки" резистора, можете да получите необходимото съпротивление, като свържете последователно няколко резистора. Както виждате, това е полезна техника.
За да удължите живота на батериите, те могат да бъдат свързани паралелно. Според закона на Ом напрежението ще остане същото (можете да проверите това, като измерите напрежението с мултицет). "Животът" на една двойна батерия ще бъде значително по-дълъг от този на две заместващи се клетки.
Моля, обърнете внимание: Паралелно могат да се свързват само захранвания с един и същ потенциал. Това означава, че изтощени и нови батерии не трябва да се свързват заедно.
Ако ги свържете, батерията с по-голям капацитет ще се стреми да зарежда батерията с по-малък капацитет. В резултат на това общият размер на таксата им ще спадне до ниска стойност.
Като цяло това са най-често срещаните употреби на тези връзки.
Идеален източник на електродвижеща сила
Електромоторната сила (E) е физична величина, която определя степента, в която външните сили влияят върху движението на носителите на заряд в затворена верига. С други думи, ЕМП определя колко ток ще протече през проводника.
Когато обясняват подобни неразбираеми явления, учителите в родното училище обичат да се позовават на метода на хидравличните аналогии. Ако проводникът е тръба, а електрическият ток е количеството вода, което тече през нея, то ЕМП е налягането, което помпата развива, за да изпомпва течността.
Терминът "електродвижеща сила" е свързан с напрежението. Тя, ЕМП, също се измерва във волтове (единица "V"). Всеки източник на енергия, независимо дали е батерия, генератор или слънчев панел, има своя собствена електродвижеща сила. Често тази ЕМП е близка до изходното напрежение (U), но винаги е малко по-малка от него. Това се дължи на вътрешното съпротивление на източника, върху което неминуемо пада част от напрежението.
Поради тази причина идеалният източник на ЕМП е по-скоро абстрактно понятие или физически модел, който няма място в реалния свят, тъй като вътрешното съпротивление на електрическата клетка, Rvn, макар и много ниско, все пак е различно от абсолютната нула.
Идеален и реален източник на ЕМП
В диференциална форма
Формулата често се представя в диференциална форма, тъй като проводникът обикновено е хетерогенен и трябва да бъде разбит на възможно най-малко участъци. Токът, който протича през него, е свързан с големината и посоката, така че се счита за скаларна величина. Когато е необходимо да се намери резултантният ток през проводник, се взема алгебричната сума от всички отделни токове. Тъй като това правило се прилага само за скаларни величини, токът също се приема за скаларна величина. Известно е, че през сечението протича ток dI = jdS. Напрежението върху него е равно на Edl, тогава за проводник с постоянно сечение и еднаква дължина съотношението ще бъде вярно:
 Диференциална форма
Диференциална форма
Следователно изразът за тока във векторна форма е: j = E.
Важно: При металните проводници проводимостта намалява с увеличаване на температурата, докато при полупроводниците тя се увеличава. Законът на Ом не показва строга пропорционалност
Съпротивлението на голяма група метали и сплави изчезва при температура, близка до абсолютната нула, а процесът се нарича свръхпроводимост.